Lataa tulostuskelpoinen PDF-versio tästä luvusta koneellesi!

Porrasmalli 

Lähimmän naapurin menetelmä

Liukuvien keskiarvojen menetelmä

Ripley, B. D. 1981. Spatial Statistic. Wiley series in probability and mathematical statistics. New York

Trendipintamenetelmä

Splinifunktiot

Porrasmalli

Porrasmalli on yksinkertainen epäjatkuvan tasoituspinnan tuottava interpolointimenetelmä. Siinä pyritään määrittämään tasoituspinnan rajalinjat siihen kohtaan, jossa ominaisuuden arvo muuttuu.  Rajalinjat rajaavat alueita, joissa ominaisuuden arvo on likimain sama. Menetelmä tuottaa porraskuvan, jossa kunkin alueen arvo voidaan kuvata arvoa vastaavana portaana (kuva 1). Siirryttäessä alueelta toisella on noustava tai laskeuduttava askelma. Menetelmä perustuu oletukseen, että ominaisuuden arvo muuttuu hyppäyksittäin rajalinjaa ylitettäessä eikä vaihtele alueiden sisällä.

Luonnonprosesseissa tämä oletus pitää kuitenkin harvoin paikkaansa. Menetelmä soveltuu luokka-asteikollisten muuttujien interpolointiin ja olosuhteisiin, joissa joudutaan käsivaraisesti tasoittamaan jonkin ominaisuuden vaihtelua (Burrough 1987). 

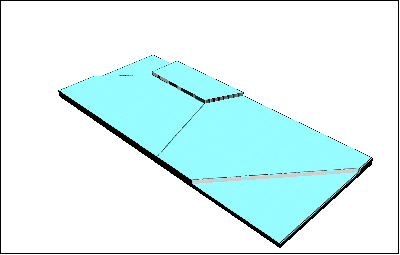
Kuva 1. Porrasmallitekniikalla on rajattu kohdealueelta 5 aluetta Porrasmallissa portaan korkeus kuvaa ominaisuuden arvoa, joka keskimäärin vallitsee alueella.

Lähimmän naapurin menetelmä

Porrasmallitekniikan keskeinen ongelma on, miten rajata alueet havaintopisteiden ympäriltä.  Ongelma on pyritty ratkaisemaan esimerkiksi  Lähimmän naapurin menetelmällä.  Menetelmä perustuu alueenmuodostustekniikan käyttöön, joka tunnetaan nimellä Voronoin polygonit (Thiessen-polygonit, Dirichlet-solut) 

Voronoin polygonit rajaavat kunkin havaintopisteen ympärille alueen, jonka sisällä kaikki pisteet ovat lähimpänä kyseistä havaintopistettä. Voronoin polygonit saadaan piirtämällä keskinormaalit havaintopistenaapureita yhdistäville janoille.

Kuva 2. Voronoin polygonit epäsäännölliselle  pisteverkolle.

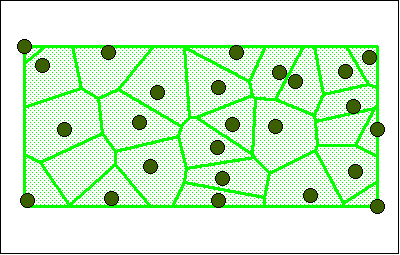
Interpoloinnissa kaikki polygonin sisällä sijaitsevat pisteet saavat sitten havaintopisteen arvon.

Menetelmän ongelmia ovat:

• Ennusteen arvo riippuu vain yhdessä havaintopisteessä mitatusta arvosta.

• Voronoin polygonit ovat riippuvaisia havaintopisteverkosta, ts. siitä, kuinka havaintopisteet on sijoitettu kohdealueelle. 

• Menetelmä ei kuvaa alueiden sisäistä vaihtelua. 

Vaikka kunkin alueen sisälle havaintoarvolle estimoidaan sama arvo, on Voronoin polygonit kuitenkin paras interpolointimenetelmä luokka-asteikollisten tunnusten  interpoloimiseksi.

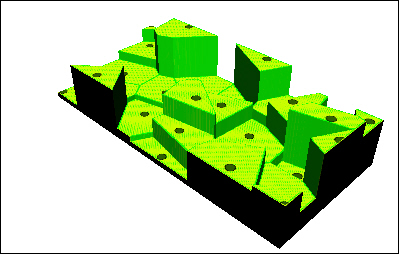
Kuva 3: Edellisen kuvan Voronoin polygoneja käyttävä porrasmalli

Voronoin polygoneja sovelletaan usein  yhdistettynä johonkin kehittyneenpään menetelmään. Luonnollinen naapuruus -nimellä (eng. natural neighbourhood) tunnetussa menetelmässä tekniikkaa sovelletaan liukuvien keskiarvojen menetelmässä tarvittavien painojen määrittämiseen. Voronoin polygoni -tekniikkaa voidaan soveltaa myös splin-tasoituksessa tarvittavien osa-alueiden määrityksessä.   

Liukuvien keskiarvojen menetelmä

Liukuvien keskiarvojen menetelmä. on yksinkertaisin jatkuvan ennustepinnan tuottava interpolointimenetelmä. Siinä kohdepisteelle lasketaan arvo ympäristön havaintojen painotettuna keskiarvona. Painot lasketaan havaintopisteiden ja kohdepisteiden välisen etäisyyden funktiona seuraavan kaavan  mukaisesti (Ripley 1981). 

Yleensä painofunktion arvo lähenee ääretöntä, kun havaintopisteen ja kohdepisteen välinen etäisyys lähestyy nollaa.

Menetelmää sovellettaessa käytetään myös lähimpien havaintojen lukumäärään perustuvaa painofunktion määritystä, jolloin menetelmää voidaan kutsua n lähimmän naapurin menetelmäksi. Käytännössä tiettyä maksimietäisyyttä kauempana olevat painot määritellään nolliksi. Jos maksimietäisyyttä lähempänä ei kuitenkaan ole yhtään havaintoa, siirretään kohdepisteelle lähimmän havaintopisteen arvo.

Liukuvien  keskiarvojen menetelmän etuja ovat:

• Yksinkertaisuus ja helppo laskennallinen toteutus.  

• Pystytään ottamaan huomioon myös pienimuotoinen paikallinen vaihtelu, kun valitaan painofunktion parametrit sopivasti.  

Liukuvien keskiarvojen menetelmän heikkoutena on herkkyys havaintopisteiden ryhmittäisyydelle. Mikäli kohdepistettä lähellä on samalla etäisyydellä ryhmä havaintopisteitä ja toisaalla taas yksittäinen havainto, painottuvat ryhmän havaintopisteet interpoloinnissa liikaa. Menetelmä soveltuu siis suhteellisen tasaisin välein sijoittuvien havaintopisteiden avulla kerättyjen aineistojen interpolointiin. 

Käänteisneliömenetelmä (eng. inverse square distance interpolation, IS) on liukuvien keskiarvojen-menetelmän erikoistapaus, jossa painofunktio w=d^-2. Joskus näistä käytetään myös nimitystä "painovoimafunktiot". 

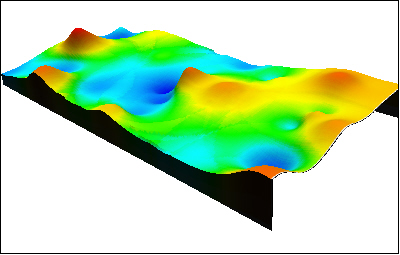
Kuva 4. IDW-menetelmällä (liukuvien keskiarvojen menetelmän erikoistapaus) luotu pinta samasta aineistosta, josta edellisen kuvan Voronoi-porraskuvio oli piirretty.

Trendipintamenetelmä

Yksinkertaisin tapa kuvata asteittaisia muutoksia on mallittaa niitä polynomiregressiolla. Ajatuksena on sovittaa viiva tai pinta pienimpien neliösummien avulla niin, että pinta tai käyrä poikkeaa mahdollisimman vähän havaintoarvoista. Spatiaaliset koordinaatit X ja Y oletetaan selittäjiksi ja kiinnostuksen kohde Z on selitettävä muuttuja (Burrough 1987). Menetelmä soveltuu hyvin laaja-alaisen, hitaasti vaihtuvan vaihtelun mallintamiseen. Se ei ota huomioon pienialaista paikallista vaihtelua.

Yksinkertaisin tapa yksiulotteisessa aineistossa mallittaa ominaisuutta Z on käyttää lineaarista regressiota

                                                                                                                                                                           missä Z on mallitettava ominaisuus ja X muodostuu havaintopisteistä, b0 ja b1 ovat parametrejä. Kaksiulotteisessa aineistossa otetaan mukaan myös Y-koordinaatti. Tuloksena on taso, joka kulkee havaintopisteen kautta. 

Epälineaarisen vaihtelun mallittamisessa voidaan käyttää korkeamman asteen polynomifunktiota (Burrough 1987), jolloin tuloksena on (polynomifunktion asteluvusta riippuen) käännepisteitä sisältävä pinta. 

Trendipintamenetelmän heikkouksia ovat:

• Reunavaikutus, jolloin interpoloitavan alueen rajojen lähellä ekstrapoloidut arvot voivat olla epärealistisia. 

• Joustamattomuus pienillä asteluvuilla. 

• Korkeamman asteen polynomifunktioiden termien merkitysten tulkinta on vaikeaa. 

• Mikäli havaintopisteitä on vähän, voivat ääriarvot vääristää estimoitua pintaa voimakkaasti. 

• Menetelmällä tuotettu ennustepinta ei kulje havaintopisteiden kautta eli menetelmä tuottaa pehmennetyn ennusteen havaintoaineistosta. 

Regressiotekniikkaan perustuva trendipintamenetelmä on helppo ymmärtää ja ohjelmallisesti helppo toteuttaa. Menetelmää käytetään usein mallintamaan koko tutkimusalueen laaja-alainen vaihtelu ennen paikallisen interpolointimenetelmän käyttöä (Tokola ja Kalliovirta 2003).

Splinifunktiot

Splinit ovat paloittaisia funktioita, jotka sovitetaan tarkasti muutamaan havaintopisteeseen kerrallaan. Samanaikaisesti varmistetaan, että käyrän osien liiittymäkohdat ovat jatkuvia (Burrough 1987). Splinien avulla on mahdollista muokata käyrän osaa ilman, että koko käyrää tarvitsee laskea uudelleen.

Splini-nimeä käytettiin ensimmäisen kerran menetelmälle, jossa paloittaisen kuutiopolynomifunktion (piecewise cubic polynomial) avulla tasoitettiin havaintoaineisto jatkuvaksi käyräksi, jolla on jatkuva 1. ja 2. derivaatta (Burrough 1987). Menetelmässä aineisto jaetaan "paloihin", ja jokaisessa "palassa" aineistoon sovitetaan kolmannen asteen polynomifunktio niin, että se ei muodosta epäjatkuvuuskohtaa liittyessään seuraavan "palan" polynomifunktioon. Myöhemmin splini-nimi laajennettiin koskemaan myös edellä kuvatusta menetelmästä johdettuja interpolointimenetelmiä. (Tokola ja Kalliovirta 2003)

Paloittaisen polynomifunktion p(x) yleinen määritelmä on: 

Funktiot pi(x) ovat polynomifunktioita (Burrough 1987). Splinejä voidaan käyttää sekä tarkkaan interpolointiin että karkeaan tasoittamiseen (Burrough 1987). Kolmiulotteisessa tapauksessa, kun halutaan ennustaa pinta havaintopisteiden avulla, voidaan käyttää niin sanottuja B-splinejä, jotka koostuvat kukin useasta pienemmästä splini-funktiosta (Burrough 1987). B-splinejä voidaan kuvata pieninä mäkinä ja laaksoina, joita yhdistelemällä saadaan kuvattua haluttu pinta.

Splinifunktioiden käytön etuja ovat:

• Koska splinifunktiot käsittelevät aineistoa pala kerrallaan, on interpolointi nopeaa. 

• Tasoitettu pinta voidaan määrätä kulkemaan tarkalleen havaintopisteiden kautta tai pinta voidaan pehmentää keskimääräiseksi tasoitukseksi, joka ei mukaile kaikkia äärihavaintoja. 

• Menetelmällä pystytään ottamaan huomioon myös pieniä paikallisia piirteitä tarkemmin kuin esim.  liukuvien keskiarvojen menetelmässä. 

Splini-menetelmän tarvitsemien parametrien määrääminen on hankalaa:

• Minkä verran ennustepinta saa poiketa havaintoarvoista?

• Palojen koko?

• Onko osavälien raja havaintopisteiden välissä vai kohdalla? 

Nämä parametrit vaikuttavat oleellisesti siihen, minkälaisen ennustepinnan menetelmä tuottaa. Menetelmä ei myöskään tuota suoraan arviota estimoidun pinnan luotettavuudesta.

• Geostatistiset interpolointimenetelmät (Kriging)

• Takaisin etusivulle

Boolen operaattorit leikkausanalyysissä

Tehtävä: Tee kuvan "leikkaustyypit" mukaiset leikkaukset paikkatieto-ohjelmallasi. Mikäli käytät MapInfo-ohjelmistoa, löytyvät toiminnot valikon "Kohteet" alta.

Huomaa, että saatat joutua suorittamaan monta erillistä leikkausoperaatiota halutun lopputuloksen saavuttamiseksi. Loppukäyttäjille tarkoitetuissa käyttöliittymissä usein tarvittavat leikkausanalyysit tavallisesti automatisoidaan.