Lataa tästä tulostuskelpoinen PDF-versio

Perustuu teoksiin:

Tokola ja Kalliovirta: Paikkatietoanalyysi.

Helsingin Yliopiston metsävarojen käytön laitoksen julkaisuja 34.

Kainulainen, S. J. 2002:
GIS-palvelinteknologian hyödyntäminen luonnonvarojen tilastollisessa tarkastelussa. Lisensiaattityö. Teknillinen korkeakoulu. 

Kohteidenvälinen topologia

Kohteidenvälisiä suhteita eli topologiaa voidaan tarkastella menetelmällä, jossa verrataan samanaikaisesti leikkaamalla kohteiden ulkopuolta (eng. exterior, Ø), sisäpuolta (eng. interior, i) ja kohteita rajaavaa vektorigeometriaa (eng. boundary, ¶). Vertailujen tuloksena voidaan laatia taulukossa 3.2 kuvattu leikkausmatriisi, jossa leikkauskombinaatiot esitetään yhdeksässä matriisin alkiossa eli solussa.  

Taulukko 3.2. Kohteidenvälinen 9-leikkausmatriisi (Kainulainen 2002).

Solujen arvot lasketaan vertailevina joukko-operaatioina, jolloin solu voi saada arvokseen loogisen arvon (tosi tai epätosi) tai laskennallisen operaation tuloksena on tyhjä tai osajoukko geometriaa. Sijainnillisesti dimensioidussa tarkastelussa otetaan huomioon lisäksi leikkauksen tuloksena syntyvän geometrian vapausasteet, jolloin solun arvona on Æ (ei leikkausta), 0 (yhteinen piste), 1 (yhtyvä viivasegmentti) tai 2 (päällekkäinen alue). 

Topologiasuhteita käytetään yleensä kohteiden hakulausekkeiden vertailuissa. OGC on määritellyt viisi tarkasteltavaa tapausta eli predikaattia. Seuraavissa kaavoissa esiintyvä merkintä dim() tarkoittaa leikkauksen dimension määrittämistä sekä P, L ja A vastaavia piste-, viiva- ja aluegeometrian joukkoja. R tarkoittaa kaikkia mahdollisia geometrioita:

1.      1.  Kohteet ovat erillään (disjoint). Mikään osa kohteen a geometriasta ei kosketa kohdetta b. Joukko-opillisesti esitettynä

a.Disjoint(b) Û a Ç b =  Æ

2.      Kohteet koskettavat (touches). Kohteet eivät peitä toisiaan, mutta toisen kohteen rajalla oleva piste yhtyy toisen kohteen rajaviivaan. Joukko-opillisesti esitettynä

  a.Touches(b) Û ( I(a) Ç I(b) =  Æ ) Ù ( a Ç b) ¹ Æ ,

missä (a Î R Ù b Ï P) Ú (a Ï P Ù b Î R).

3.      Kohteet risteävät (crosses). Piste- tai viivageometria risteää viiva- tai aluegeometriaa, jos piste on viivan päällä tai alueen sisällä tai jos viiva leikkaa toisen viivan tai alueen rajan.

a.Crosses(b) Û (dim( I(a) Ç I(b) < max(dim(I(a)), dim(I(b)))) Ù ( a Ç b) ¹ a Ù ( a Ç b) ¹ b

missä (a Î P Ú a Î L) Ù (b Î L Ú b Î A).

4.  Kohde sisältyy toiseen (within). Kohde a sisältyy kohteeseen b, jos kohde b peittää kohteen a täydellisesti. Kohteen a geometriataso on sama tai alhaisempi kuin kohteella b.

a.Within(b) Û ( I(a) Ç I(b) = Æ ) Ù ( a Ç b) = a

5.     Kohteet peittävät toisiaan (overlaps). Kohteet a ja b peittävät toisensa, jos niiden välinen leikkaus ei ole tyhjä ja niiden geometriataso on sama.

a.Overlaps(b) Û ( dim(I(a)) = dim(I(b)) = dim(I(a) Ç I(b)) ( a Ç b) ¹ a Ù ( a Ç b) ¹ b  

Tapaukset ovat toisensa poissulkevia ja kattavat kaikki topologiset tapaukset. Edellisten lisäksi on käyttömukavuuden vuoksi johdettu predikaatit sisältää (contains) ja leikkaa (intersects) seuraavasti:

a.Contains(b) Û b.Within(a)

a.Intersects(b) Û ! a.Disjoint(b)

Vertailumenetelmä on toteutettu standardeissa joko tapauskohtaisina vertailuoperaattoreina tai yleisellä relate-tarkastelulla. Relate-toiminto ottaa parametreinä tarkasteltavien geometrioiden lisäksi vertailumatriisin ja palauttaa matriisilla kuvatun vertailun totuusarvon. (Kainulainen 2002).

• Tietokantahaut

• Takaisin etusivulle

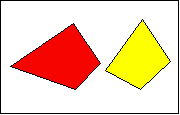
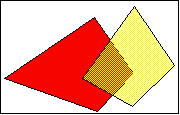
 1. Kohteet ovat erillisiä

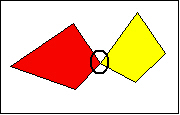
2. Kohteet koskettavat toisiaan. Niiden välinen leikkaus on piste

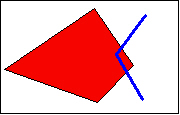
 3. Kohteet  risteävät

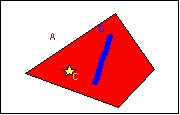
4. Alue A sisältää pisteen C ja viivan B

5. Alueet leikkaavat toisiaan.