Diskreetti ominaisuusmuutos tarkoittaa karttaobjektin ominaisuuden selvärajaista muutosta toiseksi. Esimerkiksi tilan omistaja vaihtuu tilanrajalla, kunnan nimi kunnan rajalla jne.

3.3.1 Vektorianalyysin perusmenetelmät   

Overlay-analyysi

Vektorianalyysin overlay-analyysillä tarkoitetaan karttatasojen päällekkäin asettelua ja vastinkohteiden ominaisuuksien vertailua tai yhdistämistä. Viiva- ja aluekohteiden tapauksessa analyysi johtaa kohteiden leikkauspisteiden laskentaan ja uusien alueiden muodostamiseen. Uusille alueille muodostuu joukko attribuutteja l. ominaisuustietoja. 

Overlay-analyysin tuloksena syntyy usein hyvin paljon pieniä alueobjekteja, joista jokaisella on oma yhdistelmänsä alkuperäisten tasojen ominaisuuksista. Tulosta joudutaan usein suodattamaan esimerkiksi alueen koon perusteella. Toinen mahdollisuus on jatkaa analyysia poimimalla kiinnostavat alueet jonkun ominaisuuskyselyn avulla. 

Mikäli overlay-analyysia käytetään eri lähteistä saatujen aineistojen käsittelyyn, on niiden esikäsittely useimmiten välttämätöntä. Esimerkiksi sama rajaviiva on lähes poikkeuksetta digitoitu hieman eri paikkaan (kuva 4, viereinen palsta). Analyysissa syntyy suuri määrä alueita, joiden pinta-ala on hyvin lähellä nollaa. Tämä hidastaa laskentaa, ja suurentaa tiedostokokoa ratkaisevasti. Pienten alueiden suodatus pois tuloksesta on siis tarpeen. Analysoijan täytyy kuitenkin ratkaista, kumpi rajaviivoista on luotettavampi. 

Naapuruusanalyysi

Naapuruusanalyysillä tarkoitetaan puskurivyöhykkeiden määritystä. Pisteiden, viivojen ja alueiden ympärille voidaan laskea vyöhykealue, jolla on tietty yhtenäinen ominaisuus. Uusia vyöhykealueita voidaan käyttää edelleen overlay-operaatioissa ja hauissa. Tyypillisiä vektorinaapuristoanalyysejä ovat myös ”point-in-polygon” ja ”line-in-polygon”-haut. 

Thiessen-polygonien laskenta eli vaikutusalueiden laskenta pisteille on myös naapuruutta kuvaava laskenta. Thiessen-polygoneja on käytetty kuvaamaan esim. puiden vaatimaa kasvutilaa. Lineaarinen interpolointi vektoripisteiden välille voidaan suorittaa muodostamalla TIN-pinta (kuva 5), jolla saadaan laskettua välialueiden arvojen estimaatit. 

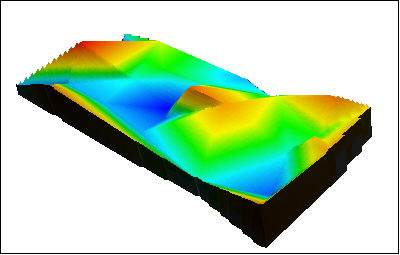
Kuva 5. TIN-pinta

Yhdistävyysanalyysi

Yhdistävyysanalyysillä tarkoitetaan kumulatiivisesti laskettavaa funktiota, jota lasketaan analysoitavan aineiston läpi kuljettaessa. Tällaisia tyypillisiä vektoripohjaisia analyysejä ovat kahden pisteen välinen etäisyys ja lyhin/nopein reitti viivaverkossa. Hydrologisen mallinnuksen jokiin ja uomiin liittyvät simuloinnit analysoidaan tyypillisesti vektoriverkossa.  

• Topologia

• Takaisin etusivulle

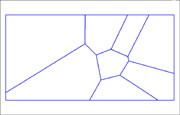
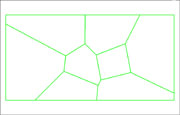
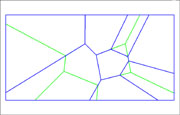
Kuvat 1-3. Overlay-analyysissä alueobjektien määrä kasvaa nopeasti. 

Kuva 4 (Alla). Eri lähteistä saadut aineistot ovat harvoin yhteneviä