2.4 Rasteripinnan luonti

Konversiot vektorista rasteriksi ja päinvastoin ovat usein tarpeen paikkatietoaineistoja analysoitaessa ja  visualisoitaessa.

Hajapisteaineistosta luotava jatkuva pinta on jo sellaisenaan analyysitulos.
 
 
 
 

Miksi rasteriksi?

Skannauksen lisäksi voimme luoda rasteriaineistoja muuntamalla vektoriaineistojamme rasteriaineistoiksi. Tämä on usein käytetty tapa ennen analysointia ja tiedostojen käsittelyä. Rasteriaineistojen analysointiin tarkoitetut ohjelmat ovat usein edullisia ja niiden analyysivälineet monipuolisempia kuin vektoriaineistoja käsittelevissä ohjelmistoissa. 

Myös tilanteissa, joissa osa analyysissä käytettävistä aineistoista on valmiiksi rasterimuotoista, on vektorimuotoiset alueita sisältävät aineistot yleensä tarkoituksenmukaisinta muuttaa pikselikooltaan vastaaviksi rasteriaineistoiksi.

Joskus rasteroinnin tuloksena syntyvä jatkuva pinta on jo sinänsä kiinnostava ilmiön maantieteellistä jakaumaa havainnollistava analyysitulos.

Kun vektoriaineistoja muunnetaan rasteriaineistoiksi, on huomattava, ettei pistemäisillä tai viivamaisilla kohteilla ole pinta-alaa. Yleensä niille on rasterointia varten ensin määritettävä halutun säteinen puskuri (buffer), joka sitten rasteroidaan. 

Yleisin tapa muodostaa vektoriaineistosta rasteriaineisto on ns. hilatiedoston muodostaminen. Hilatiedosto on säännöllinen n*m - ulotteinen pistematriisi, jossa jokainen piste saa ominaisuustiedoiksi ne tiedot jotka pisteen kohdalla olevalla rasteroitavan  aineiston aluekohteellakin on. Mikäli alkuperäinen aineisto koostuu hajapisteistä, interpoloidaan tai mallinnetaan hilapisteen arvo jollain menetelmällä alkuperäisten pisteiden arvojen perusteella.   

Kun hilan pisteille on laskettu arvot, muodostetaan rasteri, jossa jokaisen pikselin keskipisteeksi tulee em. hilatiedoston piste. Rasterin arvoksi tulee joku hilapisteiden lasketuista ominaisuustiedoista. Jos alkuperäisen vektoriaineiston alueilla on kymmensarakkeinen ominaisuustiedosto, voidaan siitä muodostaa kymmenen rasteritiedostoa, joissa rastereilla on erilaiset arvot.

Rasteripinnan luomiseksi vektoriaineiston päälle, täytyy siis ensin luoda hilatiedosto. Hilapisteiden  tiheys ja niiden saamat arvot arvot riippuvat vektoritiedoston rakenteesta, halutusta resoluutiosta sekä valitusta interpolonti- tai  mallinnusmenetelmistä. Myös käyttäjän tarpeet ohjaavat hilatiedoston muotoa. Eräs tärkeimmistä valinnoista on se, sallitaanko syntyvän pinnan ylittää tai alittaa alkuperäisen datan lokaaleja maksimi- ja minimiarvoja.

Hilatiedoston pisteiden arvojen laskemiseksi on kaksi perusmenetelmää: Interpolointi ja mallinnus. Interpolointitekniikoissa hilapisteiden arvot määritetään ympäröivien pisteiden arvojen perusteella, kun taas mallinnustekniikoissa pyritään luomaan matemaattinen malli, jota pinta noudattaa.

Interpolointimenetelmät

1. Liukuvan keskiarvon tekniikka (Inverse Distance Weighing)

Menetelmässä  lasketaan pisteen arvo tietyn säteen sisään jäävien pisteiden arvojen etäisyydellä painotettuna keskiarvona. Säteen ja/tai pisteiden määrän valitsee käyttäjä. Myös etäisyyden painottava vaikutus voi olla suoraviivainen tai eksponentiaalinen. Menetelmä soveltuu hyvin tilastollisin menetelmin kerätyn datan esittämiseen, mutta sen tuloksena syntyvä pinta jättää huomioimatta alkuperäisdatan lokaaleja maksimi- ja minimiarvoja.   

Menetelmästä on edelleen kehitetty ns. Kriging-tekniikoita, joissa IDW-menetelmää tarkennetaan alkuperäisaineiston jakaumaa koskevan tilastollisen analyysin avulla. Kriging-tekniikat kykenevät löytämään spatiaalisesti jäsentynyttä dataa, kuten esimerkiksi malmisuonia.

2. Pyöristetty kolmiointi (Triangulation with Smoothing)

Tyypillinen pyöristettyä kolmiointia käyttävä työtapa on korkeusmallin (DEM) luominen korkeuskäyräaineistosta. Työvaiheet ovat seuraavat:

• Luodaan käyrästöstä hajapistetiedosto. Pisteinä käytetään joko alkuperäisiä digitoituja pisteitä , tai ne lasketaan käyriltä tasavälein. Pisteet saavat korkeusarvokseen alkuperäisen käyrän korkeusarvon.

• Hajapistetiedosto kolmioidaan yhdistämällä kukin piste kolmeen lähimpään pisteeseen. Kolmioinnissa käytetään ns. Delaunayn kriteeriä (minkä tahansa syntyvän kolmion ympäri piirretty ympyrä ei sisällä toisen kolmion sivua). Kärkipisteiden x-, y- ja z-koordinaattien avulla muodostetaan kullekin kolmiolle tason yhtälö.

• Asetetaan hilapisteverkko kolmioverkon päälle, ja lasketaan tason yhtälöiden avulla kullekin hilapisteelle korkeusasema. Muodostetaan rasteri, jossa jokainen pikseli saa korkeusarvoksi hilapisteelle lasketun korkeusarvon.

• Sovitetaan lasketun rasterin päälle pinta, joka "pehmentää" maiseman luonnolliseksi. Pinta kuvataan yleensä viidennen asteen polynomilla. Käyttäjä voi valita, hyväksytäänkö alkuperäisten arvojen lievä alittaminen tai ylittäminen pyöristyksen tuloksena.

3. Nelikulmiointerpolointi (Rectangular Interpolation)

Menetelmä perustuu nelikulmioihin, jotka muodostetaan yhdistämällä neljä hilapistettä lähimmäksi osuvaa datapistettä. Hilapisteen arvo lasketaan muodostuneiden yhdistysjanojen kaltevuuksien perusteella. Tuloksena saadaan tiukasti alkuperäisen datan arvoihin sidottu, mutta joskus kulmikas pinta.

4. Luontaisen alueen menetelmä

Luontaisen alueen menetelmä perustuu datapisteiden ympäri muodostettaviin ns. Thiessenin monikulmioihin. Monikulmio rajataan siten, että rajalta pisteeseen on aina lyhyempi matka kuin mihinkään muuhun aineiston pisteeseen. Monikulmion ominaisuustietojen arvoiksi annetaan alkuperäisten pisteiden arvot. 

Thiessenin monikulmiot ovat aluekohteita, jotka voidaan rasteroida suoraan. Rasterin arvoksi tulee tällöin joku alkuperäisten pisteiden ominaisuustieto.

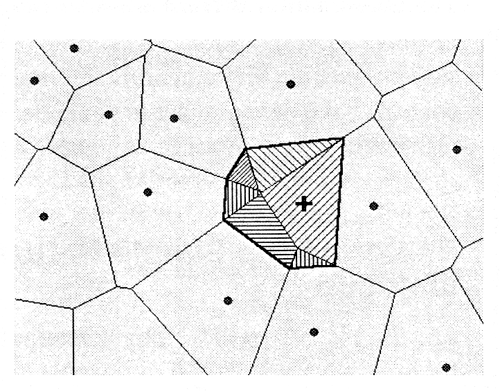
Hilapisteiden arvot voidaan interpoloida piirtämällä niille uudet Thiessenin monikulmiot. Hilapisteen arvo lasketaan suhteessa alkuperäisten monikulmioiden peittyviin pinta-aloihin (vrt. kuva).

Syntyvä pinta voidaan myös pyöristää käyttämällä apuna viereisten kuvioiden gradienttieroa. 

Mallinnus  

1. Sijaintiprofiili (Location Profiler)

Menetelmä laskee hilapisteen arvon sen keskimääräisenä etäisyytenä havaintopisteisiin nähden. Tulospintaa voidaan käyttää havainnollistamaan esimerkiksi havaintopisteiden alueellista jakautumista.

Havaintopisteiden määrää voidaan säädellä määräämällä huomioon otettaviksi esimerkiksi haluttu prosentuaalinen osuus havaintopisteistä. Myös etsintäsäde voidaan määrätä.

Joku pisteeseen liittyvä ominaisuustieto voidaan määrätä etäisyyden painokertoimeksi. Myös etäisyys voidaan ottaa huomioon lineaarisesti tai eksponentiaalisesti.

2. Kauppa-alueen mallinnus

Kauppa-alueen mallinnuksessa käytetään useita tekniikoita. Niiden tarkoituksena on selvittää tietyn palvelun, kaupan tms. vetovoima käyttäen lähtötietona kohteen maantieteellistä asemaa, aseman suhdetta kilpaileviin palveluihin ja jotain attrraktio- eli vetovoimatekijää, kuten kauppaliikkeen kokoa, hintatasoa, valikoimaa jne. 

Yleisimmin käytetään ns. Huffin malleja, joissa kauppaliikkeen tms. vetovoiman asiakkaaseen nähden oletetaan vähenevän suhteessa etäisyyden toiseen potenssiin.

• Rasterianalyysit

• Takaisin rasteritietomallin aloitussivulle

Inverse Distance Weighing-menetelmästä enemmän: ftp://ftp.geog.uwo.ca/SIC97/
Tomczak/Tomczak.html)

Huff-malli perustuu seuraaviin Newtonin fysiikasta tuttuihin oletuksiin:

• Objektin vetovoima on verrannollinen massaan
  

• Objektin vetovoima on kääntäen verrannollinen sen etäisyyteen