
Lataa tulostuskelpoinen PDF-versio tästä luvusta koneellesi!
Nykyaikaisissa GIS-ohjelmistoissa on vakiovarusteenakin joukko erilaisia interpolointimenetelmiä. Niitä on yleensä mahdollista hankkia lisää erilaisten analyysityökalupakettien mukana. Yleensä niiden käyttö on helppoa, mutta oikean menetelmän valinta ja tuloksen luotettavuuden arviointi vaatii perustietoja menetelmästä ja aineistosta.
3.5.1 Johdanto
Paikkatietojärjestelmän käyttö perustuu sijainniltaan tunnetun tiedon käyttöön. Tieto ei kuitenkaan aina ole alueellisesti kattavaa, joten esimerkiksi tunnettujen pisteiden välisten alueiden kuvaamiseksi joudutaan käyttämään spatiaalisen interpoloinnin menetelmiä.
Joskus kiinnostuksen kohteena
olevan ominaisuuden arvo voidaan mitata suoraan kaikilta alueen
pisteiltä. Esimerkiksi kaukokartoitusmateriaalia tulkittaessa
menetelläänkin usein näin. Useimmiten on kuitenkin mahdotonta
havainnoida ominaisuuden arvo suoraan kaikkialta, koska tutkittavan
ominaisuuden mittaus voi olla työlästä, aikaa vievää ja/tai
kallista. Tällöin joudutaan turvautumaan näytteeseen l.
mittauspisteverkkoon, jonka tiheys ja koko riippuu budjetista ja
halutusta luotettavuudesta..
Spatiaalisessa interpoloinnissa paikkaan sidottua havaintopistetietoa käyttämällä muodostetaan interpoloimalla joko jatkuva pinta tai tihennetään olemassa olevaa pisteverkkoa. Uusille pisteille lasketaan arvot alkuperäisten havaintojen perusteella.
Lämpötila,
ilmanpaine, typpipitoisuus peltomaassa tai säteily ydinvoimalan läheisyydessä
ovat esimerkkejä tunnetusta pisteestä mitatusta pistetiedosta.
Spatiaalisen interpoloinnin ajatuksena on käyttää mitattuja arvoja
tunnetuissa pisteissä ja ennustaa arvot mitattujen pisteiden välisille
alueille.
Spatiaalinen interpolointi perustuu havaintoon, että lähellä toisiaan sijaitsevien pisteiden arvot ovat suuremmalla todennäköisyydellä lähellä toisiaan kuin kauempana olevien pisteiden arvot (Burrough 1987). Ilmiötä nimitetään spatiaaliseksi autokorrelaatioksi. Spatiaalisissa interpolointimenetelmissä pyritään mallintamaan ominaisuuden spatiaalinen autokorrelaatio tutkimusalueella ja käyttämään tätä mallia hyväksi ennustettaessa ominaisuusarvoja tuntemattomille pisteille.
Ongelmana on sopivan interpolointimenetelmän valinta. Menetelmän tulee soveltua kyseessä olevan ominaisuuden mallintamiseen ja sen tulee pystyä hyödyntämään tehokkaasti käytettyä havaintopisteverkkoa. Jotkut menetelmät soveltuvat paremmin laaja-alaisen trendinomaisen vaihtelun kuvaamiseen, toiset taas pienimuotoisemman paikallisen vaihtelun mallintamiseen.
Myös havaintopisteiden määrä ja niiden sijoittuminen tutkittavalle alueelle vaikuttavat interpolointimenetelmän valintaan. Osa menetelmistä soveltuu hyvinkin pienen havaintomäärän mallintamiseen, toiset taas edellyttävät tietyn vähimmäismäärän havaintopisteitä toimiakseen luotettavasti. Eräät interpolointimenetelmät soveltuvat paremmin systemaattisesti sijoitetun koealaverkon avulla mitattujen havaintojen tasoittamiseen, kun toiset taas soveltuvat paremmin satunnaisesti sijoittuvien havaintojen interpolointiin. (Tokola&Kalliovirta 2003)
Useimmissa interpolointimenetelmissä oletetaan, että tarkasteltava tekijä muuttuu tasaisesti ja että sitä voidaan kuvata matemaattisesti määritellyn pinnan avulla. Interpolointimenetelmiltä voidaan vaatia:
-
Ajallista ja alueellista jatkuvuutta,
-
Kohdepisteen tarkkaa maantieteellistä sijaintia
-
Pientä keskivirhettä
Deterministinen vai geostatistinen menetelmä?
Interpolointi on mahdollista tehdä joko deterministisellä tai geostatistisella interpolointitekniikalla. Molempiin tekniikoihin sisältyy erilaisia menetelmiä. Deterministiset menetelmät käyttävät interpolointiin matemaattisia funktioita. Geostatistiset menetelmät käyttävät sekä matemaattisia että tilastollisia menetelmiä. Geostatististen menetelmien etu on niiden kyky tuottaa tietoa ennusteen luotettavuudesta
Globaaliset ja paikalliset
menetelmät
Interpolointimenetelmät voidaan jakaa myös globaalisiin ja paikallisiin menetelmiin (Burrough 1987). Globaalisissa menetelmissä ominaisuuden vaihtelua kuvaavassa mallissa käytetään tarkasteltavan alueen kaikkien pisteiden havaintoja, paikallisissa menetelmissä käytetään vain naapuripisteiden havaintoja. Yleensä valitaan jokin maksimietäisyys, jota lähempänä olevat pisteet otetaan tasoitukseen mukaan.
Tunnetuimpia interpolointimenetelmiä ovat:
Globaalisia menetelmiä:
-
Trendipinta-analyysi
-
Fourier-sarjat
Paikallisia menetelmiä:
-
Splinit
-
Liukuvien keskiarvojen menetelmä
-
Kaksoislineaarinen interpolointi
-
Kriging (paikallisia menetelmiä)
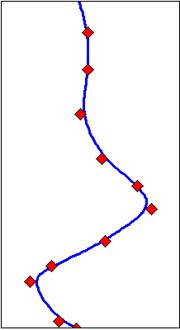
Pisteiden arvojen perusteella interpoloitu korkeuskäyrä. Huomaa, että käytetyssä menetelmässä käyrää ei ole pakotettu kulkemaan alkuperäisten mittauspisteiden kautta.
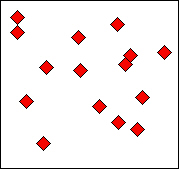
Pistetietoa voidaan mitata satunnaisesti (yläkuva) tai systemaattisesti (alakuva) sijoitetulta koealaverkolta

Burrough, P. A. 1987. Principles of Geographical Information Systems for Land Resources Assessment. Monographs on Soil and Resources Survey No 12. Oxford Science Publications.
Lisätietoja:
Tokola ja Kalliovirta 2003. Paikkatietoanalyysi. Helsingin yliopiston metsävarojen käytön laitoksen julkaisuja 34