Lataa tulostuskelpoinen PDF-versio tästä luvusta koneellesi!

Kriging-menetelmän kehittivät geologian ja kaivosteollisuuden käyttöön Georges Matheron ja D.G. Krige  1971.

Deterministiset menetelmät perustuvat suoraan ennustettavan pisteen ympäristön mitattuihin arvoihin tai matemaattisiin funktioihin, jotka määrittelevät ennustepinnan muodon. Toinen tapa interpoloida pinta paikkaan sidotun havaintopistetiedon avulla on käyttää hyväksi tilastollisia malleja, jotka huomioivat aineiston autokorrelaation l. havaintojen yhteisvaihtelun lähellä sijaitsevien havaintopisteiden kanssa. Näiden geostatististen menetelmien avulla saadaan ennustepinnan lisäksi myös tietoa ennusteen luotettavuudesta.

Kriging

Kriging-menetelmät on spatiaalinen interpolointimenetelmäperhe, jossa perusajatus on, että analysoimalla ominaisuuden spatiaalinen vaihtelu ja mallintamalla se, voidaan kullekin havaintopisteelle määrätä optimaalinen paino ennustepintaa laskettaessa (Tokola ja Kallioniemi 2003). 

Kriging-menetelmä eroaa liukuvien keskiarvojen menetelmästä siinä, että ryhmittäisyyden vaikutus otetaan automaattisesti huomioon ja ryhmän havaintoarvot saavat pienemmän painon, kuin vastaava yksittäinen havaintoarvo Kriging-menetelmässä havaintoarvojen painot määrätään alueellisen l. spatiaalisen vaihtelun perusteella.  

Kriging perustuu oletukseen, että spatiaalinen vaihtelu voidaan esittää kolmen komponentin avulla, jotka ovat: 

1. Rakenteellinen komponentti, jota voidaan kuvata pysyvällä keskiarvolla tai trendinomaisella vaihtelulla.

2. Satunnainen spatiaalisesti korreloitunut komponentti.

3. Satunnainen spatiaalisesti korreloimaton komponentti (kohina), johon voi sisältyä myös mittausvirhe (kuvat 1 ja 2).

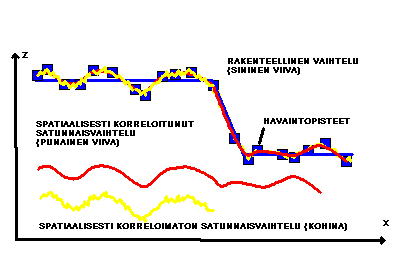
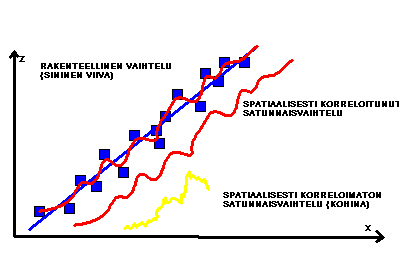
Kuvat 1 ja 2. Spatiaalisen vaihtelun komponentit tapauksissa, joissa rakenteellinen vaihtelu on äkillistä (kuva 1) tai trendinomaista (kuva 2) (Burrough 1987).

Tavallisessa krigingissä (eng. ordinary kriging) rakenteellinen komponentti kuvataan koko tutkimusalueen keskiarvona, kun taas universaalissa krigingissä (eng. universal kriging) rakenteellinen komponentti kuvataan sijainnin funktiona. Se voi siis vaihdella alueen eri osissa.

Seuraavassa käydään läpi ordinary kriging- menetelmän vaiheet:

 Semivariogrammin laskeminen:  Autokorrelaation olemassaoloa sekä sen ominaisuuksia tarkastellaan semivariogrammin avulla. Kahden toisiaan lähellä olevien pisteiden arvojen erotus on pienempi kuin toisistaan kaukana sijaitsevien pisteiden arvojen erotus. Semivariogrammin avulla tutkitaan, kuinka kaukana toisistaan olevat pisteet korreloivat keskenään eli ovat spatiaalisesti autokorreloituneita.  

Menetelmässä muodostetaan ensiksi kaikki mahdolliset havaintoaineiston pisteparit (kuva3). Tämän jälkeen piirretään semivariogrammi piirtämällä pisteparien väliset semivarianssit koordinaatistoon etäisyyden funktiona.  

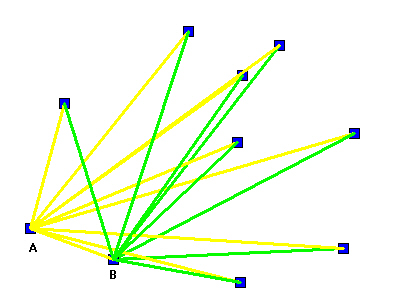
Kuva 3. Semivariogrammin laskemiseksi muodostetut pisteparit. Selvyyden vuoksi kuvaan on piirretty ainoastaan pisteille A ja B muodostetut pisteparit.

Kuten kuvasta huomataan kasvaa pisteparien määrä nopeasti havaintopisteiden lukumäärän kasvaessa. Havaintopisteparit voidaan tällöin myös luokittaa niiden keskinäisen etäisyyden perusteella. Jos luokkaväli on liian suuri, saattaa tärkeää jaksottaista vaihtelua jäädä havaitsematta. Tasavälisen otoksen tapauksessa sopiva luokkaväli on usein havaintopisteiden välinen etäisyys. 

Semivariogrammi voidaan laskea erikseen esimerkiksi länsi-itä ja etelä-pohjoinen suunnille. Mikäli autokorrelaatio on sama joka suuntaan, sanotaan aineiston olevan isotrooppinen. Muussa tapauksessa aineistoa kutsutaan anisotrooppiseksi.  Anisotropiaa ei pidä sekoittaa globaaliin trendiin, joka voidaan mallittaa ja poistaa laskennallisesti. Anisotropia on tilastollisesti havaittavaa, mutta selittämätöntä suuntautunutta spatiaalista vaihtelua. 

Anisotropian toteamiseksi aineistoa voidaan tutkia sektori kerrallaan. Englanninkielinen termi tutkittavan alueen leveydelle on bandwidth.

Mallin sovittaminen: Malli autokorrelaatiosta saadaan sovittamalla tasoituskäyrä semivariogrammin pisteparveen (kuva 4). Pisteparveen sopivin malli saadaan, kun sovitus tehdään pienimmän neliösumman menetelmällä. Tällöin minimoidaan pisteiden ja pisteparveen piirretyn tasoituskäyrän etäisyyksien neliöiden summa. Saatu malli määrittelee aineiston spatiaalisen autokorrelaation. Tasoituskäyrinä käytetään monenlaisia funktioita.

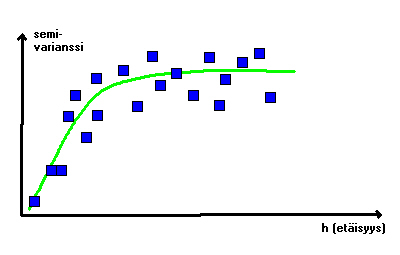
Kuva 4. Tyypillinen semivarianssin pisteparveen sovitettu semivarianssimalli.

Matriisien muodostaminen: Ordinary kriging- interpolointimenetelmä sisältää matriiseja ja vektoreita, jotka ovat riippuvaisia spatiaalisesta autokorrelaatiosta sekä pisteiden tilajakaumasta. Sovitettua autokorrelaatiomallia käytetään interpoloinnissa hyväksi määritettäessä etsintäsäde ja painot interpoloitavan pisteen naapuripisteille. Painot valitaan niin, että laskettu estimaatti on harhaton ja estimaatin varianssi on pienempi kuin minkään muun lineaarisesti muodostetun estimaatin varianssi (Burrough 1987).

Pisteen arvon ennustaminen: Laskettujen painotusten mukaan voidaan laskea ennustearvo pisteelle, jonka arvo on tuntematon. Varsinainen interpolointi tuottaa kullekin kohdepisteelle ominaisuuden arvon ennusteen lisäksi myös arvion ennustetun arvon virheestä. Näin voidaan tuottaa esimerkiksi 95 % luottamusväli ennustetulle arvolle.

Kriging-menetelmä vastaa siis tilastollisen tarkastelun avulla monien determinististen menetelmien yhteydessä esitettyyn kysymykseen kuinka kaukaa ja millaisin painotuksin naapuripisteiden arvot tulisi huomioida pisteen arvoa ennustettaessa. Teoriassa kriging- menetelmä antaa erittäin hyviä tuloksia, ja vastaa myös kysymykseen estimaatin luotettavuudesta, mutta perusoletusten paikkansapitävyys havaintoaineistossa tulee tarkastaa huolellisesti ennen menetelmän soveltamista.

• Verkkoanalyysi

• Takaisin etusivulle

Esimerkki Kriging-menetelmän soveltuvuudesta spatiaalisesti järjestyneen aineiston vaihtelun ennustamiseen. Yläkuvan havainnot voisivat olla esimerkiksi tyypillisen lounaasta koilliseen kulkevan harjumaiseman korkeusarvoja, jotka on saatu säännöllisen koealaverkon avulla.

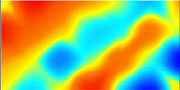
Tavalliselle TIN-menetelmään perustuvalle interpoloinnille koealaverkko on liian harva.

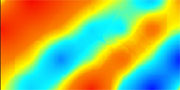
Kriging-menetelmä tunnistaa säännöllisen vaihtelun, ja piirtää oikeamman kuvan tilanteesta

Globaali trendi on esimerkiksi vallitsevan tuulen suunnasta johtuva suuntautuneisuus savukaasujen leviämisessä. Ilmiö tunnetaan, ja se voidaan mallittaa jo ennen semiovariogrammin laskemista (Tokola ja Kallioniemi 2003).