
Lataa tulostuskelpoinen PDF-versio tästä luvusta koneellesi!
0
Verkkojen tietomalli luodaan kuvamaan verkon todellisuutta ja se yleensä yritetään muotoilla niin, että sitä on helppo käyttää.
Matematiikassa verkkoja käsitellään graafiteoriassa. Verkko on graafi, johon voidaan sisällyttää myös vuorovaikutusta ja liikkumista kuvaavaa käyttäytymistä. Verkoille on ominaista, että sen osat (solmut ja viivat) voivat sisältää painoja eli ”läpivirtauskustannuksia”.
Kuljetusverkon kuvaus voi perustua joko solmu-viiva-esitykseen tai dynaamiseen segmentointiin. Verkon analysointia varten tästä geometrian kuvauksesta usein tehdään analysointia varten sopiva tietokanta. Jos halutaan tehdä yksittäisistä viivoista verkko on selvää, että viivojen virheetön liittyminen toisiinsa solmupisteissä on tärkeää (topologia).
Solmupisteiden välisiä viivoja kutsutaan myös linkeiksi (Links). Linkeissä voidaan oletusarvoisesti liikkua molempiin suuntiin. Linkin kautta kulkemisesta koituvaa kustannusta kutsutaan impedanssiksi ja siinä olevat estot ovat esteitä (barriers). Este esitetään negatiivisena impedanssina. Risteykset sijaitsevat solmupisteissä.
Kun koordinaateista ei ole tietoa, joukko toisiinsa solmuin liittyviä viivoja muodostavat loogisen verkon. Verkon tietomallin elementit ovat:
-
Solmuelementtitaulu (junction element table)
-
Viivaelementtitaulu (edge element table)
-
Liitostaulu (connectivity table)
Oikean sarakkeen kuvissa 1 ja 2 on esitetty eräs mahdollinen verkon tietomalli nimeltään Node-Node Adjacency Matrix. Tietomallissa matriisin rivit ja sarakkeet kuvaavat verkon solmuja. Nollasta poikkeavat luvut rivillä i ja sarakkeessa j kertovat verkon linkin arvon solmusta i solmuun j. Arvo nolla tarkoittaa, että solmujen i ja j välillä ei ole linkkiä.
Node-Node Adjacency Matrix -tietomallin vaatima tallennustila kasvaa verkon solmujen lukumäärän kasvaessa potenssiin kaksi. Tietomallin etuna on sen yksinkertaisuus, helppokäyttöisyys sekä sopivuus suurille verkoille. Muita mahdollisia tietomalleja ovat esim. Forward Star ja Reverse Star-tietomallit (Tokola ja Kallioniemi 2003).
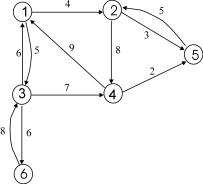
Verkko, jossa solmujen välillä on yhteyksiä ja niillä eri vastuksia.
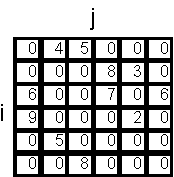
Yllä esitetyn verkon solmujen yhteyksiä kuvaava matriiisi, ns. Node-Node-Adjacency Matrix. Nollasta poikkeavat luvut kuvaavat verkon linkin vastusta solmusta solmuun. 0 taas indikoi, että yhteyttä ei ole. (Tokola ja Kallioniemi 2003).