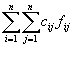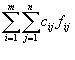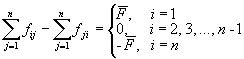Lataa tulostuskelpoinen PDF-versio tästä luvusta koneellesi!

Lyhin reitti

Tilojen ja tilasiirtymien muodostamaa verkkorakennetta kutsutaan tietojenkäsittelytieteessä  tila-avaruudeksi. Tila-avaruuden hakualgoritmit vaativat usein, että tila-avaruus on esitetty siten, että jokaisesta tilasta u voidaan muodostaa joukko Adj(u), jossa ovat ne alkiot, joihin tilasta u on olemassa tilasiirtymä. 

Tilasiirtymiin voidaan liittää paino (weight) d(u,v), joka kertoo, millainen kustannus vaaditaan kuljettaessa tilasta u tilaan v. Tilaa s kutsutaan tavallisesti lähtötilaksi  (source) ja tilaa t maalitilaksi (goal, sink). Lyhintä polkua s - t kutsutaan myös optimaaliseksi poluksi tai reitiksi. (Tuikkala 2002)  

Leveyshaku on ehkä yksinkertaisin tila-avaruuden etsintäalgoritmi. Leveyshaku etenee annetusta lähtötilasta s tasaisena rintamana käyttäen tilasiirtymiä, kunnes se saavuttaa maalitilan t. Jos kaikilla tilasiirtymillä on sama paino niin leveyshaku löytää lyhimmän reitin tilasta s tilaan t, olettaen, että t on saavutettavissa s:stä.

Tehtävissä, joissa on yleisessä tapauksessa (tilasiirtymillä erilaisia painoja) löydettävä lyhin polku s:stä t:hen, tarvitaan toisenlaista algoritmia. Eräs mahdollisuus on käyttää Dijkstran algoritmia.

Dijkstran algoritmi ratkaisee yhden lähteen lyhimmän polun ongelman painotetuille suuntaamattomille graafeille. Yhden lähteen lyhimmän polun ongelmassa on annettuna yksi lähtöpiste s ja yksi tai useampi maalipiste t. Tehtävänä on löytää lyhin polku lähtöpisteestä kaikkiin maalipisteisiin.

Leveyshakualgoritmi ylläpitää jonoa Q, jossa sijaitsevat käsittelemistä odottavat pisteet (so. etsintärintama). Kun jostain pisteestä v_i löydetään kaari johonkin toiseen pisteeseen, tämä piste siis lisätään jonon Q perälle. Jos lisäksi halutaan tietää löydetyn polun paino, on löydettyihin solmuihin algoritmin edetessä tallennettava kumulatiivinen paino (so. edellisen solmun paino johon lisätään solmujen välisen kaaren paino). Matemaattisesti asia ilmaistaan seuraavasti d(v) = d(u) + d(u,v). Käytännössä usein riittää, että lasketaan polun etäisyys lähtöpisteestä, jolloin kaava yksinkertaistuu muotoon d(v) = d(u) +1. (Tuikkala 2002).

Virtaus ruuhkautumattomien verkkojen läpi

Minimikustannusvirtaus  

Minimikustannusvirtaus on verkon virtausongelmien perustapaus. Minimikustannusvirtaus määrittelee kustannuksiltaan pienimmän reitin verkon läpi alkusolmusta loppusolmuun. Monet tärkeät virtausongelmat ovat tämän yleisen ongelman erikoistapauksia. Tällaisia analyysityökaluja on liitetty viime aikoina myös paikkatieto- ja kuljetusohjelmiin.

Oletetaan, että on olemassa suunnattu (virtaus voi kulkea vain määrättyyn suuntaan) verkko G = [N, A] seuraavin ominaisuuksin (Kuva 1):

• Virtaus tulee verkkoon tarjontasolmujen kautta ja poistuu verkosta kysyntäsolmujen kautta. 

• Tarjottu ja kysytty määrä on näissä solmuissa tunnettu. 

• Kuljetussolmut eivät tuota tai poista virtausta verkosta. 

• Kaikki virtaus, joka tulee kuljetussolmuun kulkee ainoastaan sen kautta ja lähtee eteenpäin.

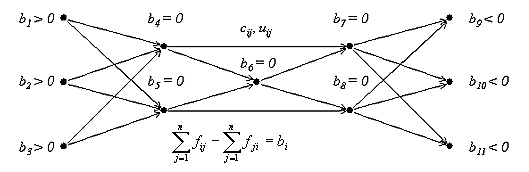
Kuva 1. Minimikustannusvirtaus

Edellisen perusteella minimikustannusvirtaus voidaan esittää minimointiongelmana (Miller & Shaw 2001):

c_ij = kahden solmun (i, j) välisen viivan virtauskustannus yksikköä kohti

u_ij = kahden solmun (i, j) välisen viivan virtauskapasiteetti

b_i = nettovirtaus solmussa i, b_i:n arvo riippuu solmun tyypistä:

b_i > 0, jos solmu i on lähtö- tai tarjontasolmu,

b_i = 0, jos solmu i on kuljetussolmu,

b_i < 0, jos solmu i on loppu- tai kysyntäsolmu,

f_ij = kahden solmun (i, j) välisen viivan virtaus.

  Rajoituksilla:

jossa n on solmujen määrä.  

Rajoituksen 1 mukaan virtauksen erotus solmusta i solmuun j on oltava yhtä suuri kuin solmun i nettovirtaus (b_i). Rajoitus 2 määrittää, että virtaus kahden solmun välillä ei voi olla negatiivinen eikä solmujen välistä kapasiteettia suurempi.

Minimikustannusvirtausta käsittelevällä ongelmalla ja sen erikoistapauksilla on kaksi tärkeää ominaisuutta. Ensimmäinen on käyvän ratkaisun ominaisuus. Käypä ratkaisu minimikustannusvirtausongelmaan on olemassa, jos

Toisin sanoen kysyntäsolmuista verkosta poistuvan virran ja tarjontasolmuista verkkoon tulevan virran pitää olla yhtä suuret. Toinen ominaisuus on kokonaislukuratkaisu. Jos sekä nettovirtaukset (b_i) että suunnatut virtauskapasiteetit (u_ij) ovat kokonaislukuja, myös optimiratkaisuksi tulee kokonaisluku. Kokonaislukuoptimointi on tarpeen tilanteessa, jossa kuljetettavat yksiköt ovat jakamattomia.

Minimikustannusvirtauksen erikoistapauksia

Kuljetusongelma

Kuljetusongelmassa on m tarjontasolmua, joista kuljetus tapahtuu n kappaleeseen kysyntäsolmuja. Merkitään tarjontasolmuja {s_i} ja kysyntäsolmuja {d_j}. Jokainen tarjontasolmu on suoraa yhteydessä kaikkiin kysyntäsolmuihin viivoilla, joiden kapasiteetti on rajoittamaton ({u_ij} = ¥). Viivojen painot {c_ij} ilmaisevat yhden yksikön kuljetuskustannuksen tarjontasolmusta i kysyntäsolmuun j. Kuljetussolmuja ei ole. (Miller & Shaw 2001) 

Kuva 2 esittää kuljetusongelmaa. Kuljetusongelman standarditulkinnassa tarjontasolmuja ovat tuotantotehtaat tai varastot ja kysyntäsolmuja varastot tai vähittäiskaupat. Kuljetusongelman avulla voidaan määrittää esim. mistä tehtaista kukin kauppa saa tuotteensa niin, että kuljetusten kokonaiskustannukset minimoituvat. 

  Rajoituksilla:

(1)
(2)
	j = 1,2,...n i = 1,2,...n
(3)	fij ³0

Käypä ratkaisu on olemassa, jos

Jos tämä ei pidä paikkaansa, yhtälöön voidaan lisätä eron tasaava dummy-muuttuja.

Kuljetusongelman laajennusta, jossa on myös välisolmuja, kutsutaan nimellä transshipment- eli siirtämisongelma (transshipment problem). Nämä välisolmut voivat toimia kuljetus-, tarjonta- tai kysyntäsolmuina. Reaalimaailmassa transshipment-ongelma voi olla tilanne, jossa tehtaista kuljetetaan tuotteita varastoihin ja niistä edelleen vähittäiskauppoihin. Matemaattisesti tämä ongelma on samanlainen minimikustannusvirtausta käsittelevän ongelman kanssa  muuten paitsi, että kahden solmun välisen viivan ei-negatiivisuus ja kapasiteettirajoitteen tilalla on nyt pelkkä ei-negatiivisuusrajoite (Miller & Shaw 2001).

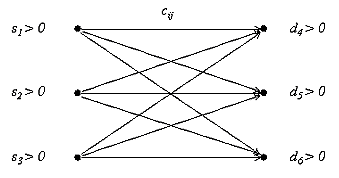
Kuva 2. Kuljetusongelma

Maksimivirtaus

Maksimivirtausongelmassa on tarkoitus löytää verkosta reitti, jota pitkin verkon läpi alkusolmusta loppusolmuun voi mennä suurin mahdollinen määrä esim. jotain tuotetta. Tässä tapauksessa on olemassa yksi tarjontasolmu ja yksi kysyntäsolmu. Näiden välillä olevat solmut ovat kuljetussolmuja. 

Koska nyt on tarkoituksena saada verkosta läpi maksimimäärä esim. jotain tuotetta kustannuksista piittaamatta, virtauskustannus{c_ij} = 0. 

Määritetään verkon läpi kulkevan virtauksen yläraja . Sekä tarjonta- että kysyntäsolmu saavat tämän arvon. Kuva 3 esittää maksimivirtausongelmaa. (Miller & Shaw 2001)   

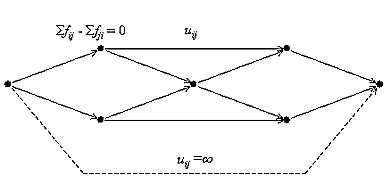
Kuva 3. Maksimivirtausongelma

Kun verkon lähtösolmu on 1 ja kohdesolmu n, voidaan maksimivirtausongelma kirjoittaa yhtälön muotoon (Miller & Shaw 2001):

  Rajoituksilla:

Minimikustannusvirtausongelman ja sen erikoistapausten ratkaiseminen

Edellä käsitellyt virtausongelmat koostuvat lineaarisista yhtälöistä. Kaikki ongelmat on muotoiltu lineaarisen ohjelmoinnin edellytysten mukaan eli sekä kohdeyhtälöt että rajoitukset ovat lineaarisia. Lineaarinen optimointiyhtälö on kätevä ratkaista simplex-algoritmin avulla. Verkon ja kuljetuksen optimoimiseksi on  olemassa omat tähän tarkoitukseen laaditut simplex-menetelmät. (Miller & Shaw 2001)

• Ruuhkautuvat verkot

• Takaisin etusivulle

Tuikkala, J. 2002. Lyhyimmän polun etsiminen ja painotettujen alueiden ongelma. Turun yliopisto. LUK-tutkielma. Tietojenkäsittelytiede. 33 s.

Miller, H. J. ja Shaw, S. 2001. Geographic information systems for transportation. Oxford University Press.